题解 P2151 【[SDOI2009]HH去散步】
题意:HH有个一成不变的习惯，喜欢饭后百步走。所谓百步走，就是散步，就是在一定的时间 内，走过一定的距离。 但是同时HH又是个喜欢变化的人，所以他不会立刻沿着刚刚走来的路走回。 又因为HH是个喜欢变化的人，所以他每天走过的路径都不完全一样，他想知道他究竟有多 少种散步的方法。
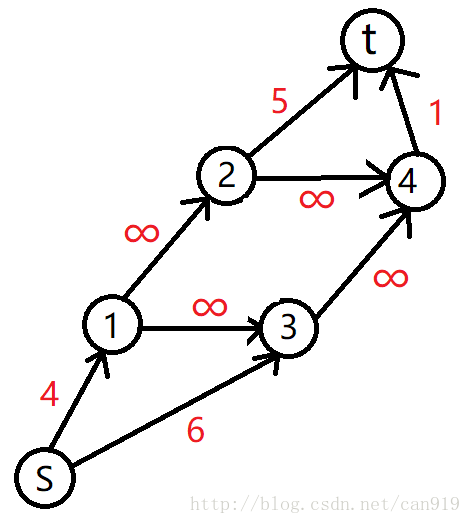
现在给你学校的地图（假设每条路的长度都是一样的都是$1$），问长度为$t$，从给定地 点$A$走到给定地点$B$共有多少条符合条件的路径
题解 CF878C Tournament
题意:最近Berland开始了一场有k种运动的比赛。瓦萨亚希望在赌场上赚钱。 比赛的计划非常神秘，并没有完全公开。比赛选手背靠背举行，每场比赛都涉及两名尚未淘汰的运动员。每场比赛都可以举行k种运动里的任意一种，失败者则遭到淘汰。最后剩下的运动员成为冠军。除此之外，该方案可以是任意的，不提前公开。 瓦西亚了解各种运动中的运动员的力量。他认为，拥有更高力量的运动员总能获胜。 比赛每年举行一次，每年都有一名新参赛者加入比赛。在第一场比赛中，只有一名运动员参加，第二场比赛有两名运动员，依此类推。 请你帮助他找到每一年可能获得冠军的人数。
网络流杂记(待填坑,可能咕咕)
求二分图最大匹配方案时只需求出所有反向边中边权大于0的即可
二分图匹配只需源点连向所有左侧的点，边权为inf，所有右侧的点连汇点，边权也为$inf$，两侧的点的连边即是原图上的连边，边权为$1$。求最大流即可
证明：
我们求最大流等于求最小割，因为两侧的点与源汇点的连边权都为$inf$，所以割边只能是
拆点
最大流模型的一般建模思路是运用流的容量限制，使得题目中的约束得以满足，有时还需使用一些特殊的方法（如拆点）来满足题目的特别约束。
拆点的主要应用
1.例如一件物品只能用有限次，但是如果不拆点普通建模跑网络流很可能会导致这个点被超过限制次数的流量经过，使答案出错，所以如果将这个点拆成两个，设为$i_1$ , $i_2$,原入边连 $i_1$，原出边连 $i_2$,$i_1$与$i_2$之间连边权为限制次数的边即可。正确性显然。
例题1:P1231 教辅的组成
例题2:P1345 [USACO5.4]奶牛的电信
(拆点解决最小割点问题)
例题: P1402 酒店之王
二分图最大匹配的三个定理
1:最大匹配数 + 最大独立集 =$n$(点数)
2:二分图的最小覆盖数 = 最大匹配数
3:最小路径覆盖 = 最大独立集
最大独立集是指求一个二分图中最大的一个点集，该点集内的点互不相连。
最小顶点覆盖是指 在二分图中，用最少的点，让所有的边至少和一个点有关联。
最小路径覆盖是指一个不含圈的有向图G 中，G的一个路径覆盖是一个其结点不相交的路径集合P，图中的每一个结点仅包含于P 中的某一条路径。路径可以从任意结点开始和结束，且长度也为任意值，包括0.
在二分图匹配时，如果有很多个条件都不满足才能连边，跑最大匹配是错误的，
网络流——最小割求最大权闭合子图
有一个有向图，每一个点都有一个权值（可以为正或负或$0$），选择一个权值和最大的子图，使得每个点的后继都在子图里面，这个子图就叫最大权闭合子图。
如下图：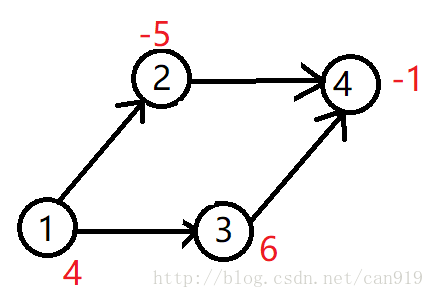
能选的子图有$Ø$(即不选),{$4$},{$3,4$},{$2,4$},{$1,2,3,4$},它们的权值分别为$0,-1,5,-6,4.$
所以最大权闭合子图为{$3,4$}，权值为$5$.
解法
这个问题可以转化为最小割问题，用网络流解决。
从源点$s$向每个正权点连一条容量为权值的边，每个负权点向汇点$t$连一条容量为权值的绝对值的边，有向图原来的边容量全部为无限大。
求它的最小割，割掉后，与源点s连通的点构成最大权闭合子图，权值为（正权值之和$-$最小割）。
如何理解
割掉一条边的含义
由于原图的边都是无穷大，那么割边一定是与源点$s$或汇点$t$相连的。
割掉$s$与$i$的边，表示不选择$i$点作为子图的点；
割掉$i$与$t$的边，表示选择$i$点为子图的点。
如果$s$与$i$有边，表示$i$存在子图中；
如果$i$与$t$有边，表示$i$不存在于子图中。
合法性
只有$s$与$t$不连通时，才能得到闭合子图。
如果$s$与$t$连通，则存在点$i,j$，使得$s$到$i$有边，$i$到$j$连通,$j$到$t$有边，所以$j$一定是$i$的后继，但选择了$i$，没有选择$j$，不是闭合子图。
如果$s$与$t$不连通，选择了正权点$i$，一定选择了$i$后继中的所有负权点。设$j$是$i$的后继中的正权点，则割掉$s$到$j$的边是没有意义的，最小割不会割掉它，则$j$一点被选中，所以$i$的所有后继都被选中，符合闭合图的定义。
最优性
最小割=(不选的正权之和+要选的负权绝对值之和）
最大权闭合子图=（正权之和-不选的正权之和-要选的负权绝对值之和）=正权值和-最小割
因为正权值和，是定值，而最小割保证值最小，所以最大权闭合子图一定最优。
例题
拓展
要求输出方案
枚举每个点的$dep$，如果$dep<inf$，那么则是方案内的点
因为那种无论怎么买花费$>$收入，这样的购买有一个特点，因为它不能供给需求，所以源点到它的残流一定是$0$，就是说不管是正向边还是反向边都是$0$，同样的那些可以供给的，源点到它的残留一定大于$0$，也就是正向边或者反向边大于$0$，说明做这个购买能赚钱。
所以在最后一遍$bfs$时，边权为$0$的边是不会走的，也就是说$bfs$时只会走边权大于$0$的边，所以走过的每一个点都是方案中的点，因为只有走过的点$dep$才会小于$inf$，所以只需要找出$dep<inf$的点即可
题解 CF632F 【Magic Matrix】
定义一个大小为 $n\times n$ 矩阵 $a$ 为魔法矩阵，当且仅当 $a$ 满足以下条件:
以下 $i,j,k\in \mathbb{Z^+}$
$\forall i\in[1,n],a_{i,i}=0$
$\forall i,j\in[1,n],a_{i,j}=a_{j,i}$
$\forall i,j,k\in[1,n],a_{i,j}\le\max(a_{i,k},a_{j,k})$
给你一个矩阵，问它是不是魔法矩阵。
如果 $a$ 是魔法矩阵输出 $\texttt{MAGIC}$，否则输出 $\texttt{NOT MAGIC}$，可以参见样例。
$1\leq n\leq 2500,\forall i,j\in[1,n],0\le a_{i,j}\le 10^9$
题解 牛客练习赛6 手铐
链接：牛客练习赛6手铐
$Description$
给你一个连通无向图，保证每个点最多属于一个简单环，每个点度数最多为$3$，求这个图有多少“手铐图形个数”
其中“手铐图形个数”，定义为三元组$(x,y,S)$，其中$x$和$y$表示图上的两个点，$S$表示一条$x$到$y$的简单路径，而且必须满足：
$1.x$和$y$分别在两个不同的简单环上
$2.x$所在的简单环与路径$S$的所有交点仅有$x,y$所在的简单环与路径$S$的所有交点仅有$y$。
$(x,y,S)$与$(y,x,S)$算同一个手铐