$Description$

给定平面上的一些点，求这些点能组成的所有三角形的面积之和

$Description$

有一个$n\times m\times l$的立方体，立方体中每个格子上都有一个数，如果某个格子上的数比三维坐标至少有一维相同的其他格子上的数都要大的话，我们就称它是极大的。

现在将$1\sim n\times m\times l$这$n\times m\times l$个数等概率随机填入$n\times m\times l$个格子（即任意数字出现在任意格子上的概率均相等），使得每个数恰出现一次，求恰有$k$个极大的数的概率。答案对$998244353$取模。

$Description$

你有一个容量为$W$的背包，和$8$种物品，重量分别为$1\sim 8$的整数，分别有$cnt_1,cnt_2\cdots cnt_8$ 个。
求背包中最多能装上多大的重量。

$Description$

给出一个$N$个点$M$条边的无向带权图，以及$Q$个询问，每次询问在图中删掉一条边后图的最小生成树。(各询问间独立，每次询问不对之后的询问产生影响，即被删掉的边在下一条询问中依然存在)

$Description$

求$01$背包前$k$优解的价值和

$Description$

给出一个$n\times n$的矩阵,每一格有一个非负整数$a_{i,j},(a_i,j\leqslant 1000)$现在从$(1,1)$出发,可以往右或者往下走,最后到达$(n,n),$每达到一格,把该格子的数取出来,该格子的数就变成$0$,这样一共走$K$次,现在要求$K$次所达到的方格的数的和最大

方法$1:$

利用$atan2()$函数按极角从小到大排序。

$atan2(double~y,double~x)$其中$y$代表已知点的$Y$坐标，同理$x$ ,返回值见下图，它的值域相应的也就是$-\pi\sim \pi$了

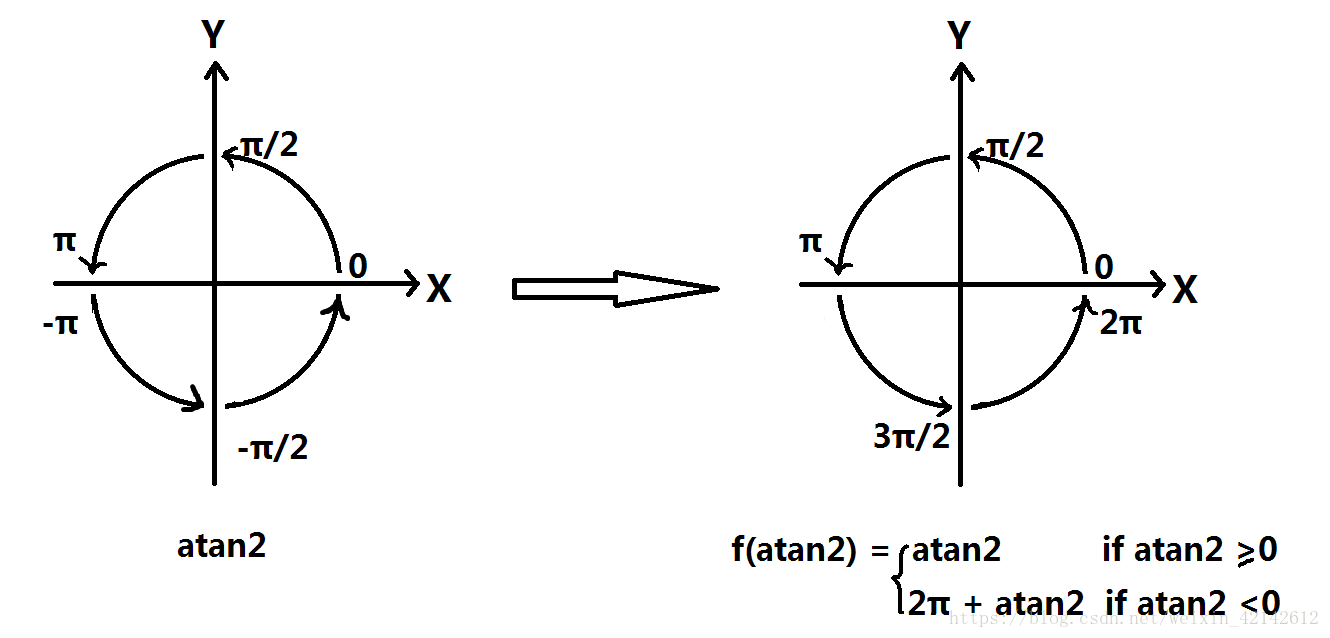
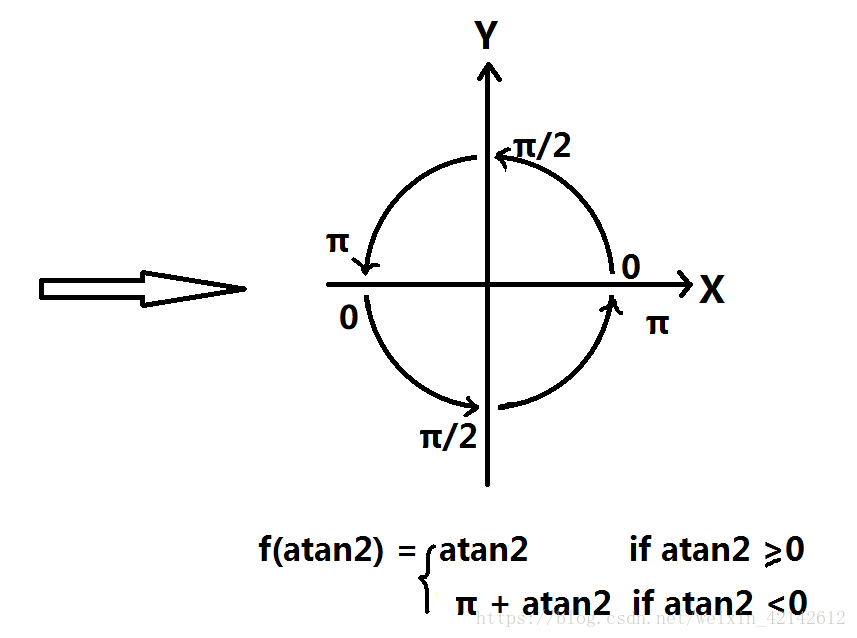
$atan2$转换到$\left[0,2\pi\right)$表示的是与$x$轴正方向的逆时针夹角，这样转换的好处是便于计算两条线之间的夹角。

第二种转换是用于对直线进行极角排序的。

1
2
3
4
5
6

bool cmp(point a,point b){
    if(atan2(a.y,a.x)!=atan2(b.y,b.x))
        return atan2(a.y,a.x)<atan2(b.y,b.x);
     return a.x<b.x;
}//不转换

方法$2:$

利用叉积。

1
2
3

friend double operator ^(Point a,Point b){
    return a.x*b.y-b.x*a.y;
}

若叉积$>0$，则向量$a$在向量$b$的顺时针方向,叉积$<0$，则向量$a$在向量$b$的逆时针方向

1
2
3
4
5

bool cmp(point a,point b) {
    if((a^b)==0)
        return a.x<b.x;
    else return (a^b)>0;
}

排序效果同单个$atan2()$

方法比较

一般情况下用叉积(精度高),但是$atan2()$更加灵活。

前置芝士$:$向量及其的基本运算，如叉积(叉积运算下面用符号^表示)。

对于一个已知三点坐标的三角形，其面积是可以算出来的。

设点$c$为原点$(0,0)$

$S_{\Delta}=\frac{|\vec{a}|\times |\vec{b}|\times\sin (\theta)}{2}=\frac{\vec{a}~\hat{}~\vec{b}}{2}=\frac{\left|x_{1}\times y_{2}-x_{2}\times y_{1}\right|}{2}$

对于任意多边形

$S=\frac{\left| \sum_{1}^{n-1}(x[i]\times y[i+1]-x[i+1]\times y[i])+x[n]\times y[1]-x[1]\times y[n]\right|}{2}$

$ps:$注意绝对值不要忘。

来张图

在网上并没有找到什么严格的证明，但是如果自己手玩过就会发现这样做是对的。

其中标出的$a$部分(不包括多边形本身)被重复算了两次，一次加，一次减，而多边形本身只被算了一次，符合题意。

如果点的坐标不是按顺序依次给出的又该怎么办呢？

$1.$所给多边形为凹包(或者不给说明，凸包和凹包都有可能)：

如果点不是按照顺序依次给出的，那么所构成的多边形一定不唯一（画画就明了），所以点一定是按顺序给出的

$2.$所给多边形为凸包：

我们可以先将点按极角排序，就可套用公式了,(凸包的点极角排序后多边形的顶点是依次有序的,且多边形一定是唯一的)

例题P2785 物理1（phsic1）- 磁通量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include <bits/stdc++.h>
#define int long long
#define re register
#define inf 0x3f3f3f3f
#define N 2000900
#define sqr(x) ((x)*(x))
#define eps 1e-6
using namespace std;
struct point{
    double x,y;
    friend point operator -(point a,point b){
    	return (point){b.x-a.x,b.y-a.y};
    }
    friend double operator ^(point a,point b){
    	return a.x*b.y-a.y*b.x;
    }
}p[N],s;
inline int read(){
    int x=0,w=0;char ch=getchar();
    while (!isdigit(ch))w|=ch=='-',ch=getchar();
    while (isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
    return w?-x:x;
}
inline bool cmp(point a,point b){
    return ((a-s)^(b-s))>0;
}
double ans,b;
signed main(){
    int n=read();scanf("%lf",&b);
    scanf("%lf%lf",&p[0].x,&p[0].y);
    for (int i=1;i<n;++i)scanf("%lf%lf",&p[i].x,&p[i].y);
    for (int i=0;i<n-1;++i)ans+=(p[i]^p[i+1]);
    ans+=p[n-1]^p[0];
    printf("%.4lf\n",ans*b*0.5);
    return 0;
}

$Description$

一次舞会有$n$个男孩和$n$个女孩。每首曲子开始时，所有男孩和女孩恰好配成$n$对跳交谊舞。每个男孩都不会和同一个女孩跳两首（或更多）舞曲。有一些男孩女孩相互喜欢，而其他相互不喜欢（不会”单向喜欢“）。每个男孩最多只愿意和$k$个不喜欢的女孩跳舞，而每个女孩也最多只愿意和$k$个不喜欢的男孩跳舞。给出每对男孩女孩是否相互喜欢的信息，舞会最多能有几首舞曲？

$Description$

给定一些冰块，每个冰块上有一些企鹅，每个冰块有一个可以从当前冰块跳出的次数限制，每个冰块位于一个坐标，现在每个企鹅跳跃力为$d$，问所有企鹅能否跳到一点上，如果可以输出所有落脚冰块，如果没有方案就打印$-1$