极角排序

发表于 | 更新于

方法$1:$

利用$atan2()$函数按极角从小到大排序。

$atan2(double~y,double~x)$其中$y$代表已知点的$Y$坐标，同理$x$ ,返回值见下图，它的值域相应的也就是$-\pi\sim \pi$了

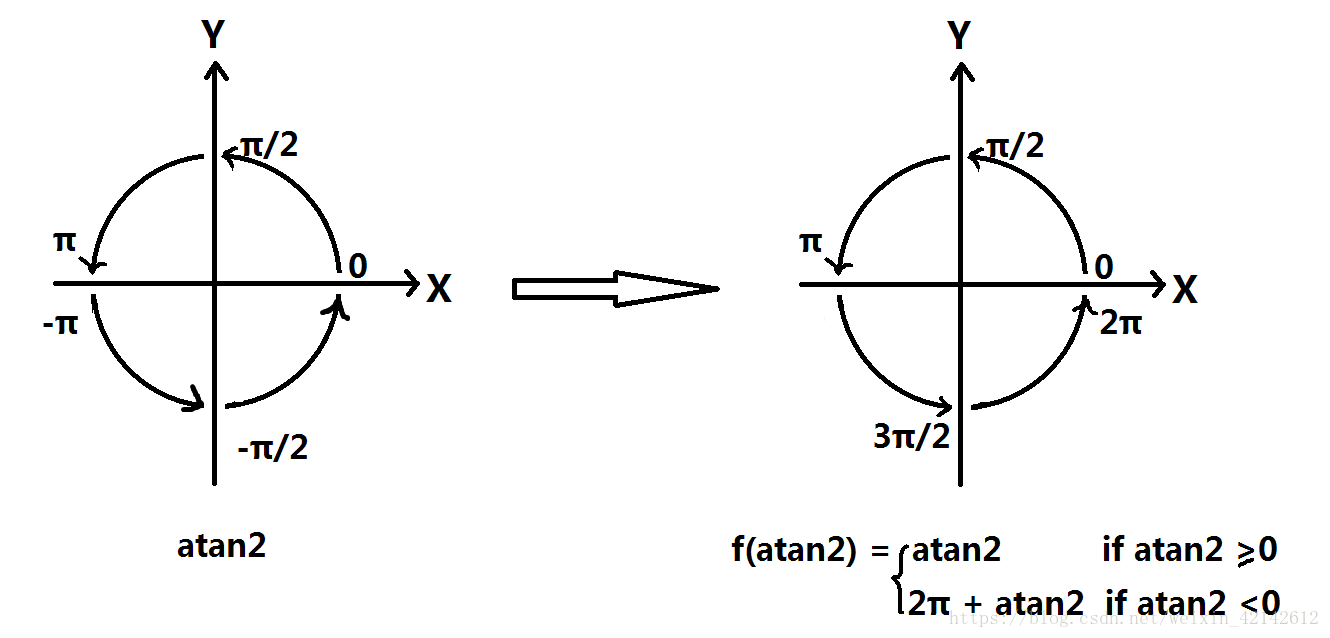
2018070916220484.png
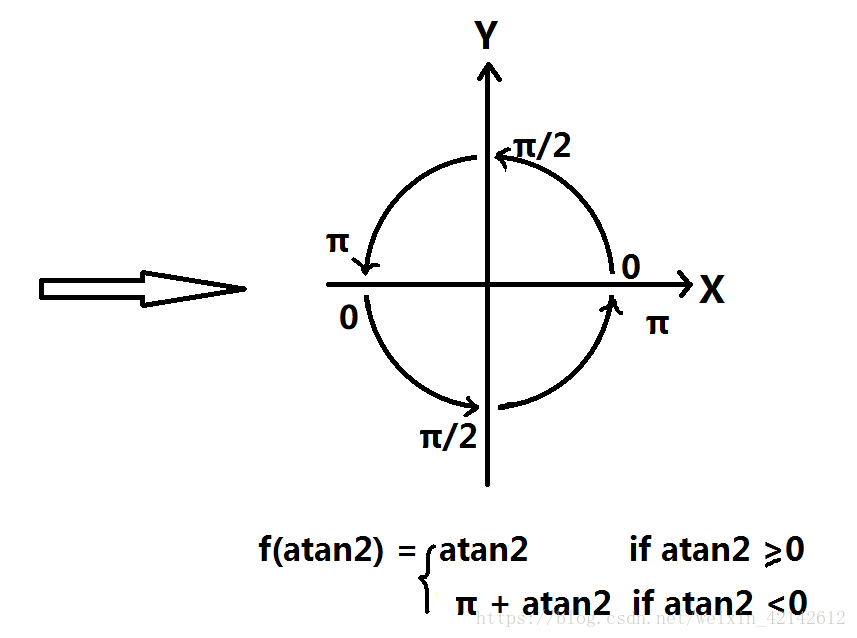
frefefrferferftgtrgy.png

$atan2$转换到$\left[0,2\pi\right)$表示的是与$x$轴正方向的逆时针夹角，这样转换的好处是便于计算两条线之间的夹角。

第二种转换是用于对直线进行极角排序的。

1
2
3
4
5
6

bool cmp(point a,point b){
    if(atan2(a.y,a.x)!=atan2(b.y,b.x))
        return atan2(a.y,a.x)<atan2(b.y,b.x);
     return a.x<b.x;
}//不转换

方法$2:$

利用叉积。

1
2
3
friend double operator ^(Point a,Point b){
    return a.x*b.y-b.x*a.y;
}

若叉积$>0$，则向量$a$在向量$b$的顺时针方向,叉积$<0$，则向量$a$在向量$b$的逆时针方向

1
2
3
4
5
bool cmp(point a,point b) {
    if((a^b)==0)
        return a.x<b.x;
    else return (a^b)>0;
}

排序效果同单个$atan2()$

方法比较

一般情况下用叉积(精度高),但是$atan2()$更加灵活。